PageRank, büyük ölçekli internet verilerinin anlaşılmasına yardımcı olmak ve araştırmacıların yeni arama teknolojilerini kolayca denemelerini sağlamak için Stanford Üniversitesi araştırma platformunda akademik bir projenin parçası olarak Larry Page ve Sergey Brin tarafından geliştirilmiştir. Brin ve Page, 1995 ile 1998 yılları arasında yapılan çalışmaları neticesinde nihayetinde Google adını alacak işlevsel bir arama motoru prototipi oluşturduğu 1998'e kadar tüm internet belgelerin içinde bir sorgu terimi ile en uygun sonucu bulmak için yapılan aramalarda sayfa içi faktörlere (On-Page Factors) bağlı çözümler kullanılmaktaydı. Bu çözümlerdeki ortak büyük problem internet’in büyüyen yapısına yetişememesi ve kalitesiz arama sonuçları sağlamasıydı. Larry Page ve Sergey Brin, bir sayfaya bağlantı veren sayfaların sayısına ve kalitesine bağlı olarak bir sayfanın (Sayfa Sıralaması) mutlak değerinin hesaplanmasını önermiştir. PageRank, Google’ın bir sayfanın önemini ölçme yöntemidir. Başlık etiketi ve anahtar kelimeler gibi diğer tüm faktörler göz önüne alındığında, Google sonuçları düzenlemek için PageRank'i kullanır. Böylece daha "önemli" olan siteler, sorgu yapan kullanıcıya gösterilen arama sonuç sayfasında buna göre ilerler (Brin ve Page, 1998; Ridings ve Shishigin, 2002).
PageRank'in Matematik İfadesi
Google’ın PageRank algoritması, internet sayfaları arasındaki bağlantıların yapısını, önemini yansıtan her sayfaya puan atamak için kullanan matematiksel bir reçetedir. Aslında, bir sayfadan diğerine giden her bağlantı, hedef sayfa için bir “oy” olarak sayılır. Her sayfanın puanı, kendisine bağlantı veren sayfaların puanlarına bağlıdır. PageRank, tüm internet sayfalarını kenarlar ve köprüler olarak oluşturduğu internetgrafı temel alan bir matematik algoritmasından güç alır. PageRank algoritması, milyarlarca internet sayfasının her birine bir PageRank puanı atar. Algoritma, idealize edilmiş rastgele sayfaları ziyaret eden bir internet sitesi sörfçüsünün davranışını modellemektedir. Bu modelde, sayfalar arasında gezinen sörfçü, rastgele olarak bir internet sayfasını seçer. Ardından, rastgele o internet sayfasından başka bir internet sayfasına olan bir bağlantıyı seçerek gezinmeye devam eder. Sörfçü, art arda gelen internet sayfalarından rastgele bağlantı seçme işlemini, başka bir internet sayfasına bir bağlantı seçmekten başka yollarla taşıma işlemi bitinceye kadar devam eder. İdealize edilmiş internet sörfçüsü, internet sayfalarını ziyaret etmekten asla bıkmaz. PageRank algoritması bu modeli kullanarak, bağlantıları rasgele tıklayan bir kişinin belirli bir sayfaya ulaşma olasılığını temsil etmek için kullanılan bir olasılık dağılımı sunmuş olur.
PageRank Algoritmasının Matris Gösterimi
PageRank, internet üzerindeki her sayfaya reel sayı atar. Atanmış değeri yüksek olan sayfa PageRank için daha önemlidir. Bu internet grafiği olarakta gösterilebilir (Şekil 1). Sayfalar node, linkler ise kenarlardır. Bir random surfer (rastgele seçim yapan kullanıcı) A düğümünde ise, B, C ve D düğümlerini seçme olasılığı 1/3’tür. A’da kalma olasılığı ise 0’dır. Bu gösterimi matris (1) olarak gösterirsek,
 |
| Şekil 1. Sayfaların bağlantı durum şeması |
 |
(1) |
|
mij = 1/k |
ise, “j” sayfada k tane dış bağlantı vardır ve bir tanesi “i” sayfaya verilmiştir. Değeri, sıfır ise link verilmemiştir.
M matrisinin her sütunundaki değerler toplamı 1’e eşittir (stokastik matris). Herhangi bir sütundaki olasılık dağılımı PageRank fonksiyonu verir.
Bir random surfer başlangıçta İnternet’teki n sayfadan birisinde başlasın. Başlangıç vektörü V0 her eleman için değerine sahiptir.
M, İnternet’teki transition matrix (geçiş matrisi) olsun. Bir adım sonraki olasılık dağılımı Mv0 olur. İki adım sonra eşitlik (2);
 |
(2) |
Random surfer’ın sonraki adımda i node’una geçme olasılığı xi değerinin hesaplama formülü (3):
 |
(3) |
vj, rastgele sörfçünün önceki adımdan node j’de olma olasılığıdır.
mij, rastgele sörfçünün j node’unda iken i node’una geçme olasılığıdır. Aşağıdaki şartlar altında v dağılımının limit değeri (4);
|
v = M × v |
(4) |
eşitliğini sağlar. Sonuçta;
- Herhangi bir node’a herhangi bir node’dan ulaşılabilir.
- Bağlantı olmayan sayfa yoktur.
v vektörüne M matrisinin özvektörü denir (principal eigenvector).
v vektörü rastgele sörfçünün uzun bir süre sonunda hangi sayfada olacağını gösterir.
Başlangıç vektörü v0 kullanılarak v vektörünün değeri belirli bir yenileme sonrası için hesaplanır. M transition matrisi ve v0 başlangıç vektörü (5):
 |
(5) |
Özvektör (Eigenvector) değerlerinin yineleme değişimi (6) gibi olur.
 |
(6) |
İlk satır değeri A düğümüne aittir ve diğerlerinin 3/2 katı çıkmıştır. Matris anlatımı ile PageRank yineleme içeren hesaplamasının anlatımı bu şekildedir (Leskovec, Rajaraman ve Ullman, 2011).
Bu olasılık, 0 ile 1 arasında sayısal bir değer olarak ifade edilir. 0,5 olasılık genellikle meydana gelen bir şeyin "%50 şansı" olarak ifade edilir. Bu nedenle, bir belgenin 0,5 PageRank değeri, rastgele bir bağlantı tıklayan bir kişinin belgeye yönlendirilmesi olasılığının %50 olduğu anlamına gelir. Ziyaret edilecek internet sayfasının seçimi, daha önce ziyaret edilen internet sayfalarına bağlı değildir. Dolayısıyla, bir internet sayfasının PageRank puanı, rastgele bir İnternet sörfçüsünün internet sayfasını görüntülemek için seçtiği olasılığı temsil eder.
Rastgele İnternet sörfçüsünün etkinliğini modellemek için PageRank algoritması, İnternet'in bağlantı yapısını yönlendirilmiş grafik olarak gösterir. İnternet sayfaları grafiğin düğümleridir ve internet sayfalarından diğer internet sayfalarına bağlantılar, hareket yönünü gösteren çizgilerdir. Yönlendirilmiş İnternet grafiği çok büyük olmasına rağmen, PageRank algoritması herhangi bir boyuttaki yönlendirilmiş grafiğe uygulanabilir (Brin ve Page, 1998).
Formül Üzerinden PageRank Hesaplama
Google, bir internet sayfasının PageRank değerini hesaplarken üç faktörü göz önünde bulundurur:
- Gelen bağlantı sayfalarının miktarı ve kalitesi;
- Her bir bağlantı sayfasındaki giden bağlantıların sayısı;
- Her bir bağlantı sayfasının PageRank değeri
Temel olan fikri formüle uygularsak, bir sayfanın asıl PageRank değerini bulmak için diğer sayfalardan gelen bu sayfaya gelen PageRank değerleri toplanır.
PR(A), Sayfa A'nın PageRank'i (PageRank’ini bulmak istediğimiz sayfa)
PR(Tn); Tn Sayfasının PageRank Değeri
C(Tn); Tn sayfasından diğer sayfalara giden bağlantı sayısıdır.
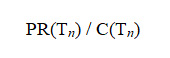 |
(7) |
Sayfa A'ya işaret eden her sayfanın PageRank değeri formül (8) ile hesaplanır. Ardından bulunan değer kazanılan toplam PageRank değeri olarak bulunacaktır. Mi, Sayfa A'ya bağlantı veren sayfaların toplam PageRank sayısı olarak belirtilir.
 |
(8) |
Basit bir düzeyde, PageRank'in nasıl hesaplandığı hakkında oldukça fazla şey söylenebilir. Bunun temel sebebi, Google’ın yalnızca bir üniversite araştırma projesi olduğu zaman, PageRank’in yaratıcıları onu hesaplamak için bu formülü tanıtan bir makale yayınladılar (Brin ve Page, 1998).
3.5.7 Rastgele Sörfçü Modeli ve Sönümleme Faktörü
PageRank, bir kullanıcı davranış modeli olarak düşünüldüğünü belirmiştik. Burada kendisine rastgele bir internet sayfası verilmiş ve sayfadaki bağlantıları tıklayıp, asla geriyi tıklamayan, ancak sonunda sıkılıp, başka bir rastgele sayfadan devam eden bir rastgele sörfçü varsayılmıştır. Bu Rastgele sörfçünün bir sayfayı ziyaret etme olasılığı PageRank’tir. Ve “d” sönümleme faktörü, her sayfada rastgele sörfçünün sıkılma ve başka bir rastgele sayfa talep etme olasılığıdır. Sönümleme katsayısı “1” değerinden çıkartılarak PageRank değerine eklenir (9).
 |
(9) |
PR(A), Sayfa A'nın PageRank'i (PageRank’ini bulmak istediğimiz sayfa) d, sönümleme faktörüdür. Nominal olarak bu 0,85 olarak alınmaktadır. Bu rakam Stanford makalesinde belirtilen değerdir (Brin ve Page, 1998).
PR(T1), Sayfa A'ya işaret eden (link veren) bir siteye ait PageRank değeridir. C(T1) bu sayfadaki bağlantı sayısıdır.
PR(Tn) / C(Tn), Sayfa A'ya işaret eden her sayfa için yaptığımız anlamına gelir. Yukarıdaki formül orijinal makalede yayınlanan formüldür.
Algoritmanın bazı varyasyonlarında (10), sönümleme faktörü (d) doküman koleksiyonundaki toplam sayfa sayısına bölünür (N) ve sonuca eklenir (Brin ve Page, 1998).
 |
(10) |
PageRank Hesaplama Uygulaması
Google teorisine göre, Sayfa A, Sayfa B'ye bağlanırsa, Sayfa A, Sayfa B'nin önemli bir sayfa olduğunu söylüyor demektir. PageRank ayrıca bir sayfaya işaret eden bağlantıların önemini de etkiler. Bir sayfanın kendisine işaret eden önemli bağlantıları varsa, diğer sayfalara olan bağlantıları da önemli hale gelir. Bağlantının asıl metni, PageRank’i tartışırken anlamsızdır. Sayfa A'yı işaret eden Sayfa B'ye verilen PageRank, Sayfa B'de bulunan herhangi bir yerdeki başka her bir bağlantıyla azaltılır. Bu, her bir sayfanın PageRank'ının esasen oy ölçütünün bir parçası olduğu anlamına gelir. Bu oylamayı bir veya iki ya da daha fazla sayı arasında bölebilir, ancak sayfanın genel oy kullanma gücü her zaman aynı kalacaktır. Sayfa B'nin PageRank değeri 5 olarak kabul edelim. Ve Sayfa A'yı işaret eden tek bir bağlantısı vardır. Sayfa A’nın PageRank değeri, Sayfa B’nin değeri 5 olan bir oranla iyileştirilir. Sayfa B hiçbir şey kaybetmez, ancak Sayfa A kazanır. B Sayfasında iki bağlantı varsa, bu PageRank iyileştirmesi bölünür ve Sayfa A, daha önce yaptığı PageRank’in yalnızca yarısını kazanır.
Diyelim ki, Sayfa A, Sayfa B, Sayfa C ve Sayfa D başlıklı, varsayımsal bir sayfa grubumuz var.
 |
| Şekil 2. Sayfaların başlangıç rank değerleri ve bağlantı durum şeması |
Başlangıç olarak, örneğimizde, sayfanın başlangıç PageRanks'ın ne olduğunu bilmiyoruz. Bu sebeple istediğimiz bir rakamı ilk PageRank değeri olarak atayabiliriz. Aslında, formül ile ilgili ilginç bir özelliği de göstermiş olacağız. Sayfalara başlangıç değeri olarak seçilen PageRank değeri, ne seçilirse seçilsin, yenileme hesaplamalarından sonra sayfaların doğru PageRank değerine ulaşmamıza bir etkisi olmamaktadır. Bu örnekte sayfaların ilk başlangıç PageRank değerini 1 olarak aldık. Ardından hesaplama için kuralları hatırlarsak:
- Bir sayfanın yeni PageRank değeri 0,85 olarak alınır. Diğer sayfalara kazandırılacak PageRank değeri, o sayfadaki bağlantı sayısına bölünerek bulunur.
- Bu miktar, geçtiği her sayfa için yeni toplamalara eklenecektir.
- Bu toplamların her birine (1-d yani 1-0,85= 0,15) olan puanı da son olarak eklenir.
Hesaplama başlangıcın da ilk yenileme hesaplaması kolaydır. Çünkü her sayfaya 1 PageRank değerini vererek başlanır.
1 × 0,85 = 0,85'dir. Böylece her sayfanın PageRank puanı 0,15 + 0,85 = 1 olur. Yani her sayfa hala 1 olan PageRank puanına sahiptir. Bu hesaplamada bağlantılara dayanarak her sayfanın önemini göstermek istiyoruz. Ama şu an için hepsinin puanı aynı; bu yüzden hesaplamayı tekrar yapmamız gerekir. İkinci yineleme hesabında, Sayfa A bu diyagrama göre Sayfa B ve Sayfa C’ye bağlantı vermektedir. Sayfa A’nın ilk hesaplama sonucu bulduğumuz yeni PageRank değeri “1”di. Bu nedenle bağlantı verdiği sayfaların yeni PageRank puanlarına 0,85 × 1 = 0,85 eklenir. Sayfa A’dan diğer sayfalara toplam iki bağlantı olduğuna göre bu puan ikiye bölünür. Böylece diğer sayfaların her biri Sayfa A’dan gelen 0,425 PageRank puanını alır. Sayfa B, Sayfa C'ye bağlanır. Sayfa B’nin başlangıç PageRank puanı 1'dir. Bu nedenle bağlandığı sayfaların yeni PageRank puanına 0.85 × 1 = 0.85 ekler. Sayfa B yalnızca sayfa C'ye bağlantı verdiğinden bu puanın tamamını Sayfa C alır. Sayfa C, Sayfa A'ya bağlanmaktadır. Bu durumda Sayfa C’ye ait PageRank, 0,85 × 1 = 0,85 olan değeri, Sayfa A kazanır. Sayfa D, Sayfa C'ye bağlanmaktadır. Bu durumda Sayfa D ya ait PageRank, 0,85 × 1 = 0,85 olan değeri, Sayfa C kazanır. Sayfa D’ye diğer sayfalar bağlantı vermemiştir. Bu durumda diğer sayfalardan artı bir PageRank puanı kazanmayacaktır. Bu durumda her sayfa için yeni toplamlar (11,12,13,14):
|
Sayfa A: 0.15 (Temel Değer) + 0,85 (Sayfa C'den) = 1 |
(11) |
|
Sayfa B: 0,15 (Temel Değer) + 0,425 (Sayfa A'dan) = 0,575 |
(12) |
|
Sayfa C: 0,15 (Temel Değer) + 0,425 (Sayfa A'dan) + 0,85 (Sayfa B'den Gelen Değer) + 0,85 (Sayfa D'den Gelen Değer) = 2,275 |
(13) |
|
Sayfa D: 0,15 (Temel Değer) + Başka Bir Sayfadan Değer Gelmedi = 0,15 |
(14) |
Sonuç ilk hesaplamaya göre biraz daha açıklayıcı olmaya başlar. Sayfa C’nin sistemdeki en önemli sayfa olduğunu görmeye başlarız. Ancak sonuçtan emin olmak için bu hesaplamaları, her sayfanın değeri artık değişmeyecek hale gelinceye kadar sürdürüyoruz. Bu yenilemelerin bir noktadan sonra sonuçların büyük oranlarda değişmeyecek duruma gelme anına “yakınsama” denmektedir. Uygulamada, Google’ın bu yakınsama sonucuna kadar beklemesine gerek yoktur. Muhtemel birkaç hesaplama yinelemesi ile sonuca geçer. Verilen örnek için tüm hesaplamaları yaparsak, 20 yenilemeden sonra yakınsama noktasına gelmekteyiz. Bu değerleri de Şekil 2.3’te gösterdiğimizde durum daha iyi anlaşılacaktır.
 |
| Şekil 3. Sayfaların yinelemeler sonrasındaki rank değer değişimi |
Son durumda sayfaların PageRank puanları, Sayfa A için 1,490, Sayfa B için 0,783, Sayfa C için 1,577, Sayfa D için 0,150 olarak ortaya konar.
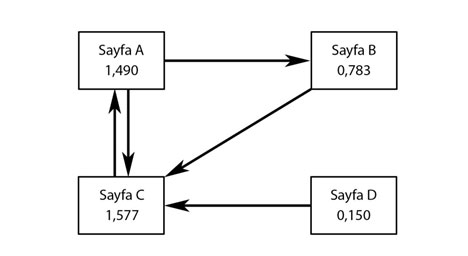 |
| Şekil 4. Sayfaların son rank değerleri |
Bu sonuçlara göre, Sayfa C’nin, bu varsayımsal sayfa grubunun en değerli sayfası olduğu kesinleşir. Sayfa A, en değerli sayfa Sayfa C’den bağlantı alması sebebi ile PageRank değerlerine göre bu grubun en değerli ikinci sayfası olmuştur. Sayfa B üçüncü sırada yer alırken, Sayfa D, hiçbir sayfadan bağlantısının olmaması sebebi sonuncu site olarak yer almıştır.
Yakınsama (Convergence)
Yakınsama, Google'ın diğer arama algoritmalarına göre üstünlük sağlayan arama kalitesini nispeten düşük maliyetlerle sunmasını sağlayan PageRank'in en önemli bir matematik yönüdür. Bu yarı karmaşık bir konudur. Ancak PageRank'in nasıl ve neden çalıştığını anlamak açısından önemlidir. Hesaplama örneğinde olabildiğince basit hale getirilerek anlatılan konu uygulamada bu derece basit olmasa da anlaşılması çok zor bir konu da değildir.
Örnek hesaplamada da gösterildiği gibi, hesaplamanın bir aşamasının çıkış değerlerinin (son değerler) bir sonraki aşamanın giriş değerleridir (başlangıç değerleri). Bu hesaplamanın sürekli yapıldığı hesaplamaya özyinelemeli prosedür olarak bilinir. Fakat asıl büyük soru, bu özyinelemeli prosedürün nasıl ve ne zaman sona ereceğine karar verilen andır. Bu sorunun cevabı “Yakınsama”dır. Sönümleme faktörünün (denklemdeki d değeri) birden fazla olması şartıyla yakınsama gerçekleşir. Bu yakınsama, temel olarak, hangi başlangıç PageRank değerleri ile başlanırsa başlansın, hesaplamayı birkaç kez çalıştırdıktan sonra aynı son PageRank değerlerine ulaşmayı garantiler. Hesaplama da daha fazla yineleme yapılsa dahi bu değerlerin artık değişmeyeceği anlamına da gelir.
Bu son değerler, sınırlayıcı değerler olarak bilinir. Sınırlama değerlerine ulaşıldığında, Google'ın artık PageRank’i hesaplamak için işlemci gücünü kullanmasına gerek kalmaz. İşlemler o noktada bitirilebilir. Bunu göstermek için 20 yinelemede kesilen işlem serisini devam ettirip ondalık gösterim kısmı detaylandırıp, 10 ondalık basamaklı olarak gösterilirse, 48. yinelemeden sonraki değer ne kadar hesaplanmaya çalışırsa çalışılsın, değerlerin değişmediği görülür. Değerler sınır değerlerde birleşirler. Gerçek uygulamada, hesaplamalar durdurmadan önce hiç değişmeyen değerleri buluncaya kadar beklemeye gerek yoktur. Sadece değerler çok anlamlı halde değişmeyene kadar beklenir (Tablo 3.1).
Tablo 1 Pagerank hesaplama yineleme tablosu
|
Yineleme |
A |
B |
C |
D |
Toplam |
|
21 |
1,4901259564 |
0,7833035315 |
1,5765705121 |
0,1500000000 |
4,00 |
|
46 |
1,4901074052 |
0,7832956473 |
1,5765969475 |
0,1500000000 |
4,00 |
|
47 |
1,4901074054 |
0,7832956472 |
1,5765969474 |
0,1500000000 |
4,00 |
|
48 |
1,4901074053 |
0,7832956473 |
1,5765969474 |
0,1500000000 |
4,00 |
|
49 |
1,4901074053 |
0,7832956473 |
1,5765969474 |
0,1500000000 |
4,00 |
|
50 |
1,4901074053 |
0,7832956473 |
1,5765969474 |
0,1500000000 |
4,00 |
|
51 |
1,4901074053 |
0,7832956473 |
1,5765969474 |
0,1500000000 |
4,00 |
|
52 |
1,4901074053 |
0,7832956473 |
1,5765969474 |
0,1500000000 |
4,00 |
|
53 |
1,4901074053 |
0,7832956473 |
1,5765969474 |
0,1500000000 |
4,00 |
|
54 |
1,4901074053 |
0,7832956473 |
1,5765969474 |
0,1500000000 |
4,00 |
PageRank Algoritmasının Fark Yaratan Noktaları
İnternet’in giderek büyüyen yapısına uyum sağlayan bağlantıya dayalı bir algoritma olması, özetle verimliliği, PageRank arama algoritmasını diğer arama algoritmalarının önüne geçirmiştir. İndeksleme temeli, metin içinden bilgi almaya dayalı (IR) algoritmalar internet’in her saniye büyüyen yapısını analiz edip indeksleme de ve doğru sonuçlara ulaşmada oldukça yetersiz kalmaya başladığı bir anda ortaya konan PageRank hızlı ve kaliteli arama sonuçları ile Google arama motoru şirketini dünyanın en büyük arama motoru şirketi yapmıştır.
Bir internet sayfasının PageRank puanı, o internet sayfasına, diğer internet sayfalarının ne kadar sayıda bağlantı verdiğine ve o bağlantı veren sayfaların da PageRank puanına bağlıdır. Bu tanımlamadan çıkan ana fikir, birincisi bir çok internet sayfasından bağlantı almanın yanısıra, PageRank’i yüksek bir internet sitesinden bağlantı almak, bağlantı alan internet sayfasının PageRank puanını yükseltecektir.
PageRank matematik hesaplamalarında yakınsama değeri bulur. Ve hesaplama yinelemelerini belli bir sayıda keserek diğer internet sayfalarına puan verme işlemine hızlıca geçebilir. Bu zaten verimli olan algoritmaya daha çok verimlilik katan bir yöntemdir. PageRank, metin içinden bilgi almaya dayalı arama algoritmalarının manipülelerine karşı daha dayanıklıdır. İnternet tasarımcıları zaten kendi yayınladıkları internet siteleri metinleri içine spam olan hareketler ile metin analizine dayalı algoritmaları kolayca manipüle edebilmekte olduğu bir dönemde ortaya çıkan PageRank, internet bağlantı yapısını kullanarak verdiği puanlama yöntemi ile adil, kaliteli sonuçlar veren ve manipüleye daha dayanıklı bir algoritma ortaya koymuştur.
PageRank kullandığı rastgele sörfçü modeli ile internet sayfalarının içeriğinden bağımsız “oylamaya” dayalı olarak daha adil bir şekilde puanlama yapabilmektedir. PageRank’in sönümleme faktörü ile indeskleme ve puanlama işlemlerin kesintisiz sürmesini sağlamıştır. Sönümleme faktörü yardımı ile rastgele sörfçü tıklanacak link kalmayan internet sayfalarında tıkanıp kalma sorununa çözüm olarak sunulmuştur (Ridings ve Shishigin 2002).
PageRank Algoritmasının Dezavantajları
PageRank algoritmasının Google’ı dünyanın en büyük arama motoru yapmasının yanında manipüleye açık noktaları sebebi ile sürekli geliştirilmiş, başka koruma algoritmaları ile desteklenmiştir. PageRank algoritmasını yanıltmak için internet tasarımcıları kendi internet sayfalarına çok sayıda dış bağlantı veren sayfa oluşturabilir. Ancak, PageRank algoritmasında bu sayfaların da önemi düşük olarak değerlendirilir. Algortima üzerinde kötüye kullanımın çok fazla yayılması sebebi ile Google 2016 yılından itibaren sayfaların halka açık olarak Pagerank değerini ilan etmekten vazgeçmiştir (Schwartz, 2016). Google bu tür bir kötüye kullanımdan kaçınmaları konusunda ısrarla webmasterları uyarmaktadır. Ve bunu deneyen pek çok sitenin PageRank etkisini engelleyen farklı yollar izlemektedir.
Temel PageRank manipülasyonlardan bazıları şunlardır;
- Benim siteme link verin, bende sizin sitenize link vereceğim gibi anlaşmalı karşılıklı bağlantılar alma.
- Komut dosyalarıyla veya ödül yöntemleri ile bağlantı sağlama.
- Aile ve arkadaş çevresi yardımıyla bağlantılar sağlama.
- Ücretsiz ve ücretli sayfa linkleri sağlayan siteler.
Sayfalara verilen PageRank değeri web tasarımcı ve uzmanlarının manipülasyonlarından dolayı alınan bu karar ile PageRank değeri arama sonuçlarındaki etkisi de düşmeye başlamıştır. Google PageRank değeri üzerindeki manipülasyonları tespit etmek ve gidermek amacı ile pek çok farklı algoritmayı ve çözümü de devreye almıştır. Yine de arama motoru optimizasyonu ile ilgilenen uzmanların PageRank algoritmasının öneminin ve etkinliğinin hala çok değerli olduğu hakkında fikir değişikliği yoktur (Google PageRank, bt).
Kaynaklar:
- Brin S. ve Page L. (1998). The anatomy of a large-scale hypertextual internet search engine. 10 Ağustos 2018, http://www-db.stanford.edu/~backrub/google.html.
- Google PageRank, (b.t.). 20 Ağustos 2018, https://ahrefs.com/blog/google-pagerank/.
- Leskovec J., Rajaraman A. ve Ullman J.D. (2011). Mining of massive datasets (2. Baskı). Cambridge: Cambridge Universty Press.
- PageRank algoritması, (b.t.). 20 Ağustos 2018, https://www.wikiwand.com/en/PageRank.
- Ridings C. ve Shishigin M. (2002). PageRank uncovered. 3 Ekim 2018, http://www.voelspriet2.nl/PageRank.pdf.



